Many engineering and science systems change over time, space, and many other dimensions of interest. In mathematics, function derivatives are often used to model these changes. However, in practice the function may not be explicitly known, or the function may be implicitly represented by a set of data points. In these cases and others, it may be desirable to compute derivatives numerically rather than analytically.
The focus of this chapter is numerical differentiation. By the end of this chapter you should be able to derive some basic numerical differentiation schemes and their accuracy.
Derivative¶
The derivative of a function $f(x)$ at $x=a$ is the limit
$$ f'(a) = \lim_{h \to 0} \frac{f(a+h) - f(a)}{h} $$
A numerical grid is an evenly spaced set of points over the domain of a function (i.e., the independent variable), over some interval. The spacing or step size of a numerical grid is the distance between adjacent points on the grid. For the purpose of this text, if $x$ is a numerical grid, then $x_j$ is the $j^{\mathrm{th}}$ point in the numerical grid and $h$ is the spacing between $x_{j-1}$ and $x_j$. The following figure shows an example of a numerical grid.
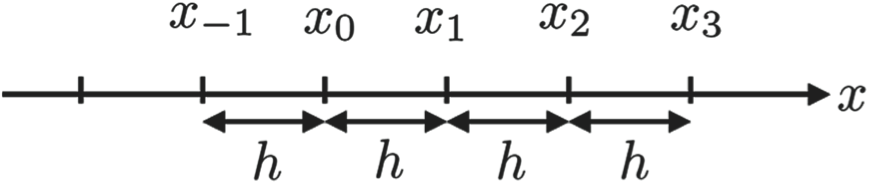
There are several functions in Python that can be used to generate numerical grids. For numerical grids in one dimension, it is sufficient to use the linspace function, which you have already used for creating regularly spaced arrays.
In Python, a function $f(x)$ can be represented over an interval by computing its value on a grid. Although the function itself may be continuous, this discrete or discretized representation is useful for numerical calculations and corresponds to data sets that may be acquired in engineering and science practice. Specifically, the function value may only be known at discrete points. For example, a temperature sensor may deliver temperature versus time pairs at regular time intervals. Although temperature is a smooth and continuous function of time, the sensor only provides values at discrete time intervals, and in this particular case, the underlying function would not even be known.
Whether $f$ is an analytic function or a discrete representation of one, we would like to derive methods of approximating the derivative of $f$ over a numerical grid and determine their accuracy.
Finite Difference Approximating Derivatives¶
The derivative $f'(x)$ of a function $f(x)$ at the point $x=a$ is defined as:
$$f'(a) = \lim\limits_{x \to a}\frac{f(x) - f(a)}{x-a}$$
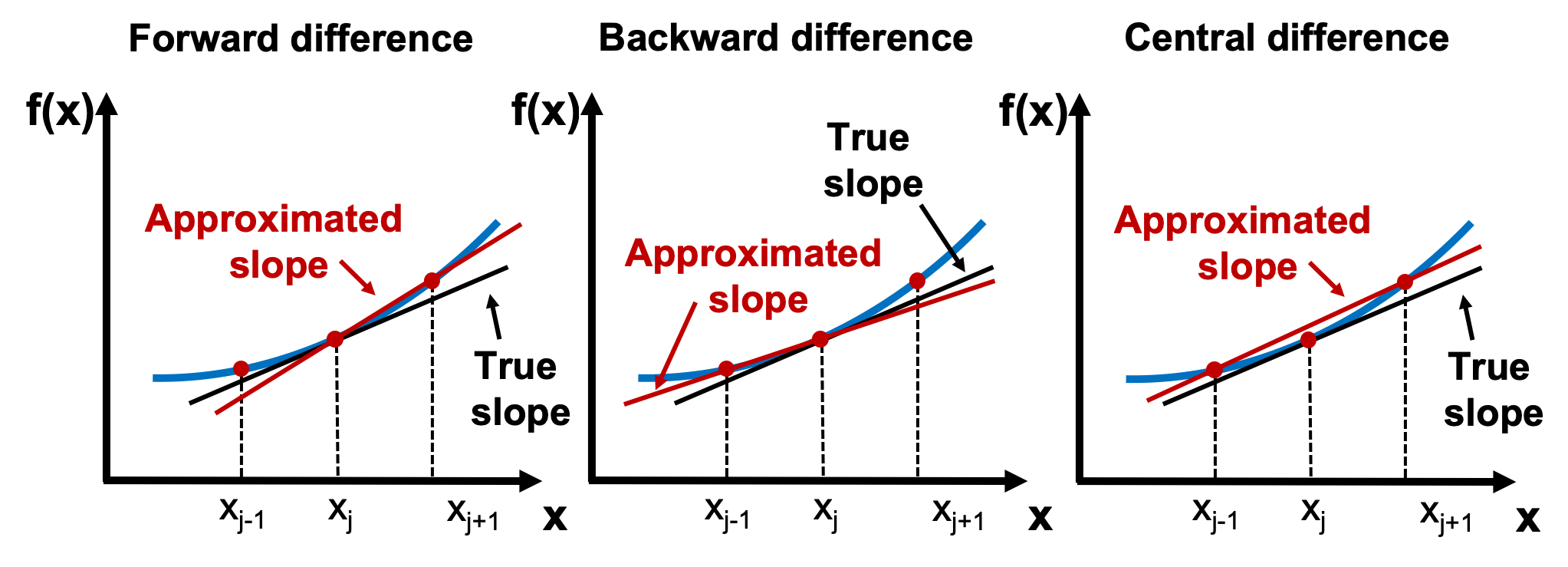
The derivative at $x=a$ is the slope at this point. In finite difference approximations of this slope, we can use values of the function in the neighborhood of the point $x=a$ to achieve the goal. There are various finite difference formulas used in different applications, and three of these, where the derivative is calculated using the values of two points, are presented below.
The forward difference is to estimate the slope of the function at $x_j$ using the line that connects $(x_j, f(x_j))$ and $(x_{j+1}, f(x_{j+1}))$:
$$f'(x_j) = \frac{f(x_{j+1}) - f(x_j)}{x_{j+1}-x_j}$$
The backward difference is to estimate the slope of the function at $x_j$ using the line that connects $(x_{j-1}, f(x_{j-1}))$ and $(x_j, f(x_j))$:
$$f'(x_j) = \frac{f(x_j) - f(x_{j-1})}{x_j - x_{j-1}}$$
The central difference is to estimate the slope of the function at $x_j$ using the line that connects $(x_{j-1}, f(x_{j-1}))$ and $(x_{j+1}, f(x_{j+1}))$:
$$f'(x_j) = \frac{f(x_{j+1}) - f(x_{j-1})}{x_{j+1} - x_{j-1}}$$
The following figure illustrates the three different type of formulas to estimate the slope.
Finite Difference Approximating Derivatives with Taylor Series¶
To derive an approximation for the derivative of $f$, we return to Taylor series. For an arbitrary function $f(x)$ the Taylor series of $f$ around $a = x_j$ is $$ f(x) = \frac{f(x_j)(x - x_j)^0}{0!} + \frac{f^{\prime}(x_j)(x - x_j)^1}{1!} + \frac{f''(x_j)(x - x_j)^2}{2!} + \frac{f'''(x_j)(x - x_j)^3}{3!} + \cdots. $$
If $x$ is on a grid of points with spacing $h$, we can compute the Taylor series at $x = x_{j+1}$ to get
$$ f(x_{j+1}) = \frac{f(x_j)(x_{j+1} - x_j)^0}{0!} + \frac{f^{\prime}(x_j)(x_{j+1}- x_j)^1}{1!} + \frac{f''(x_j)(x_{j+1} - x_j)^2}{2!} + \frac{f'''(x_j)(x_{j+1} - x_j)^3}{3!} + \cdots. $$
We are not going to cover this directly in class, but in the notebook it goes over this in more detail.
Substituting $h = x_{j+1} - x_j$ and solving for $f^{\prime}(x_j)$ gives the equation
$$ f^{\prime}(x_j) = \frac{f(x_{j+1}) - f(x_j)}{h} + \left(-\frac{f''(x_j)h}{2!} -\frac{f'''(x_j)h^2}{3!} - \cdots\right). $$
The terms that are in parentheses, $-\frac{f''(x_j)h}{2!} -\frac{f'''(x_j)h^2}{3!} - \cdots$, are called higher order terms of $h$. The higher order terms can be rewritten as
$$ -\frac{f''(x_j)h}{2!} -\frac{f'''(x_j)h^2}{3!} - \cdots = h(\alpha + \epsilon(h)), $$
where $\alpha$ is some constant, and $\epsilon(h)$ is a function of $h$ that goes to zero as $h$ goes to 0. You can verify with some algebra that this is true. We use the abbreviation "$O(h)$" for $h(\alpha + \epsilon(h))$, and in general, we use the abbreviation "$O(h^p)$" to denote $h^p(\alpha + \epsilon(h))$.
Substituting $O(h)$ into the previous equations gives
$$ f^{\prime}(x_j) = \frac{f(x_{j+1}) - f(x_j)}{h} + O(h). $$
This gives the forward difference formula for approximating derivatives as
$$ f^{\prime}(x_j) \approx \frac{f(x_{j+1}) - f(x_j)}{h}, $$
and we say this formula is $O(h)$.
Here, $O(h)$ describes the accuracy of the forward difference formula for approximating derivatives. For an approximation that is $O(h^p)$, we say that $p$ is the order of the accuracy of the approximation. With few exceptions, higher order accuracy is better than lower order. To illustrate this point, assume $q < p$. Then as the spacing, $h > 0$, goes to 0, $h^p$ goes to 0 faster than $h^q$. Therefore as $h$ goes to 0, an approximation of a value that is $O(h^p)$ gets closer to the true value faster than one that is $O(h^q)$.
By computing the Taylor series around $a = x_j$ at $x = x_{j-1}$ and again solving for $f^{\prime}(x_j)$, we get the backward difference formula
$$ f^{\prime}(x_j) \approx \frac{f(x_j) - f(x_{j-1})}{h}, $$
which is also $O(h)$. You should try to verify this result on your own.
Intuitively, the forward and backward difference formulas for the derivative at $x_j$ are just the slopes between the point at $x_j$ and the points $x_{j+1}$ and $x_{j-1}$, respectively.
We can construct an improved approximation of the derivative by clever manipulation of Taylor series terms taken at different points. To illustrate, we can compute the Taylor series around $a = x_j$ at both $x_{j+1}$ and $x_{j-1}$. Written out, these equations are
$$ f(x_{j+1}) = f(x_j) + f^{\prime}(x_j)h + \frac{1}{2}f''(x_j)h^2 + \frac{1}{6}f'''(x_j)h^3 + \cdots $$
and
$$ f(x_{j-1}) = f(x_j) - f^{\prime}(x_j)h + \frac{1}{2}f''(x_j)h^2 - \frac{1}{6}f'''(x_j)h^3 + \cdots. $$
Subtracting the formulas above gives
$$ f(x_{j+1}) - f(x_{j-1}) = 2f^{\prime}(x_j) + \frac{2}{3}f'''(x_j)h^3 + \cdots, $$ which when solved for $f^{\prime}(x_j)$ gives the central difference formula
$$ f^{\prime}(x_j) \approx \frac{f(x_{j+1}) - f(x_{j-1})}{2h}. $$
Because of how we subtracted the two equations, the $h$ terms canceled out; therefore, the central difference formula is $O(h^2)$, even though it requires the same amount of computational effort as the forward and backward difference formulas! Thus the central difference formula gets an extra order of accuracy for free. In general, formulas that utilize symmetric points around $x_j$, for example $x_{j-1}$ and $x_{j+1}$, have better accuracy than asymmetric ones, such as the forward and background difference formulas.
The following figure shows the forward difference (line joining $(x_j, y_j)$ and $(x_{j+1}, y_{j+1})$), backward difference (line joining $(x_j, y_j)$ and $(x_{j-1}, y_{j-1})$), and central difference (line joining $(x_{j-1}, y_{j-1})$ and $(x_{j+1}, y_{j+1})$) approximation of the derivative of a function $f$. As can be seen, the difference in the value of the slope can be significantly different based on the size of the step $h$ and the nature of the function.
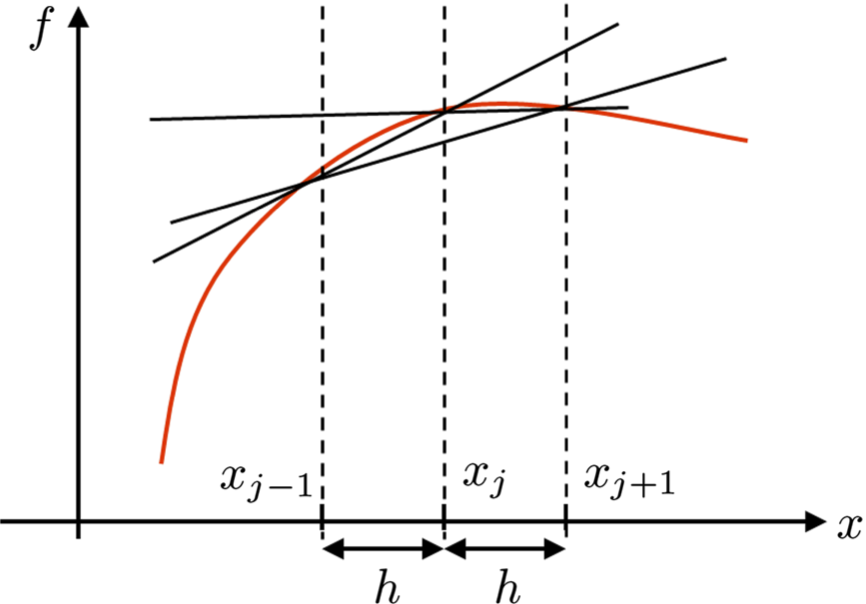
EXAMPLE¶
Consider the function $f(x) = \cos(x)$. We know the derivative of $\cos(x)$ is $-\sin(x)$. Although in practice we may not know the underlying function we are finding the derivative for, we use the simple example to illustrate the aforementioned numerical differentiation methods and their accuracy. The following code computes the derivatives numerically.
fin_diff()
0.049984407218554114
As the above figure shows, there is a small offset between the two curves, which results from the numerical error in the evaluation of the numerical derivatives. The maximal error between the two numerical results is of the order 0.05 and expected to decrease with the size of the step.
As illustrated in the previous example, the finite difference scheme contains a numerical error due to the approximation of the derivative. This difference decreases with the size of the discretization step, which is illustrated in the following example.
Example¶
The following code computes the numerical derivative of $f(x) = \cos(x)$ using the forward difference formula for decreasing step sizes, $h$. It then plots the maximum error between the approximated derivative and the true derivative versus $h$ as shown in the generated figure.
fin_diff_log()
Error Formulas¶
Natural questions arise: how good are the approximations given by the forward, backwards and central difference formulas? We derive the error formulas from Taylor's Theorem.
Again, not going to go into details on this in class, but you can read through the Theorems and Proofs on your own in the notebook.
Approximating of Higher Order Derivatives¶
It also possible to use Taylor series to approximate higher order derivatives (e.g., $f''(x_j), f'''(x_j)$, etc.). For example, taking the Taylor series around $a = x_j$ and then computing it at $x = x_{j-1}$ and $x_{j+1}$ gives
$$ f(x_{j-1}) = f(x_j) - hf^{\prime}(x_j) + \frac{h^2f''(x_j)}{2} - \frac{h^3f'''(x_j)}{6} + \cdots$$
and
$$f(x_{j+1}) = f(x_j) + hf^{\prime}(x_j) + \frac{h^2f''(x_j)}{2} + \frac{h^3f'''(x_j)}{6} + \cdots.$$
If we add these two equations together, we get
$$f(x_{j-1}) + f(x_{j+1}) = 2f(x_j) + h^2f''(x_j) + \frac{h^4f''''(x_j)}{24} + \cdots,$$
and with some rearrangement gives the approximation $$f''(x_j) \approx \frac{f(x_{j+1}) - 2f(x_j) + f(x_{j-1})}{h^2},$$ and is $O(h^2)$.
Numerical Differentiation with Noise¶
Finally, sometimes $f$ is given as a vector where $f$ is the corresponding function value for independent data values in another vector $x$, which is gridded. Sometimes data can be contaminated with noise, meaning its value is off by a small amount from what it would be if it were computed from a pure mathematical function. This can often occur in engineering due to inaccuracies in measurement devices or the data itself can be slightly modified by perturbations outside the system of interest. For example, you may be trying to listen to your friend talk in a crowded room. The signal $f$ might be the intensity and tonal values in your friend's speech. However, because the room is crowded, noise from other conversations are heard along with your friend's speech, and he becomes difficult to understand.
To illustrate this point, we numerically compute the derivative of a simple cosine wave corrupted by a small sin wave. Consider the following two functions:
$$f(x) = \cos(x)$$
and
$$f_{\epsilon,\omega}(x) = \cos(x)+\epsilon \sin(\omega x)$$ where $0 < \epsilon\ll1$ is a very small number and $\omega$ is a large number. When $\epsilon$ is small, it is clear that $f\simeq f_{\epsilon,\omega}$. To illustrate this point, we plot $f_{\epsilon,\omega}(x)$ for $\epsilon = 0.01$ and $\omega = 100$, and we can see it is very close to $f(x)$, as shown in the following figure.
x = np.arange(0, 2*np.pi, 0.01)
# compute function
omega = 100
epsilon = 0.01
y = np.cos(x)
y_noise = y + epsilon*np.sin(omega*x)
# Plot solution
plt.figure(figsize = (12, 8))
plt.plot(x, y_noise, 'r-', \
label = 'cos(x) + noise')
plt.plot(x, y, 'b-', \
label = 'cos(x)')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.show()
The derivatives of our two test functions are
$$f^{\prime}(x) = -\sin(x)$$
and
$$f_{\epsilon,\omega}^{\prime}(x) = -\sin(x)+\epsilon\omega \cos(\omega x).$$
Since $\epsilon\omega$ may not be small when $\omega$ is large, the contribution of the noise to the derivative may not be small. As a result, the derivative (analytic and numerical) may not be usable. For instance, the following figure shows $f^{\prime}(x)$ and $f^{\prime}_{\epsilon,\omega}(x)$ for $\epsilon = 0.01$ and $\omega = 100$.
x = np.arange(0, 2*np.pi, 0.01)
# compute function
y = -np.sin(x)
y_noise = y + epsilon*omega*np.cos(omega*x)
# Plot solution
plt.figure(figsize = (12, 8))
plt.plot(x, y_noise, 'r-',label = 'Derivative cos(x) + noise')
plt.plot(x, y, 'b-',label = 'Derivative of cos(x)')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.show()
Of course there are other ways we can handle noise, which we will cover later.
Definite Integrals¶
The definite integral of a function $f(x)$ over an interval $[a,b]$ is the limit
$$ \int_a^b f(x) \, dx = \lim_{N \to \infty} \sum_{i=1}^N f(x_i^ * ) (x_i - x_{i-1}) \ \ , \ x_i^* \in [x_{i-1},x_i] $$
where, for each $N$,
$$ x_0 = a < x_1 < \cdots < x_N = b $$
is a partition of $[a,b]$ with $N$ subintervals and the values $x_i^ * \in [x_{i-1},x_i]$ chosen in each subinterval is arbitrary.
The formula in the definition is not very intuitive and almost impossible to use in practice but the basic idea is simple:
$$ \int_a^b f(x) \, dx = \text{(net) area under the curve } y = f(x) \text{ on } [a,b] $$
The value of the definite integral represents the (net) area under the curve of the graph of $y=f(x)$ on the interval $[a,b]$. The term "net" means that area above the $x$-axis is positive and the area under the $x$-axis counts as negative area. For example, we can visualize the integral:
$$ \int_{\pi/2}^{3\pi/2} \left( \sin(0.2 x) + \sin(2x) + 1 \right) dx $$
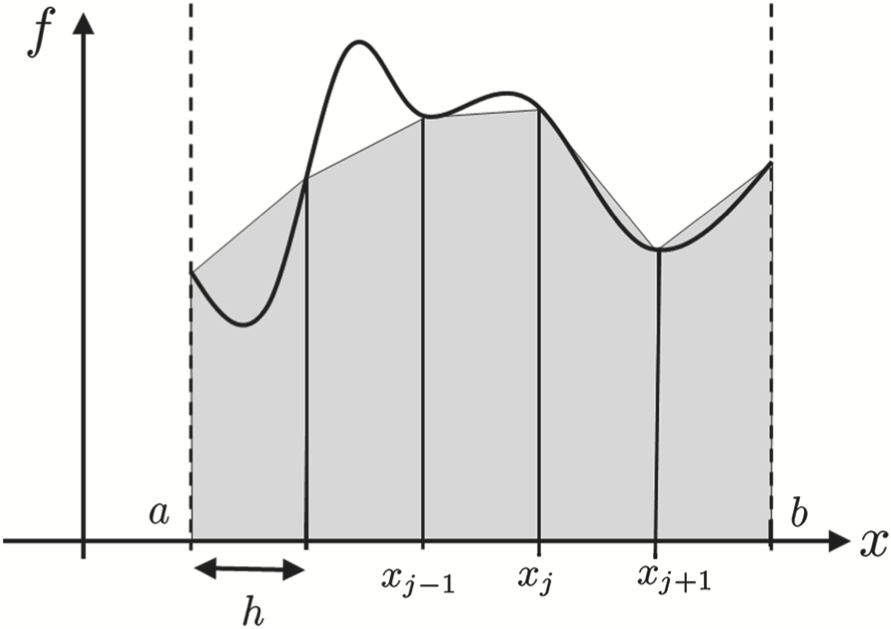
Given a function $f(x)$, we want to approximate the integral of $f(x)$ over the total interval, $[a,b]$. The following figure illustrates this area. To accomplish this goal, we assume that the interval has been discretized into a numeral grid, $x$, consisting of $n+1$ points with spacing, $h = \frac{b - a}{n}$. Here, we denote each point in $x$ by $x_i$, where $x_0 = a$ and $x_n = b$. Note: There are $n+1$ grid points because the count starts at $x_0$. We also assume we have a function, $f(x)$, that can be computed for any of the grid points, or that we have been given the function implicitly as $f(x_i)$. The interval $[x_i, x_{i+1}]$ is referred to as a subinterval.
f = lambda x: np.sin(0.2*x) + np.sin(2*x) + 1
x = np.linspace(0,2*np.pi,100)
y = f(x)
plt.plot(x,y)
X = np.linspace(np.pi/2,3*np.pi/2,100)
Y = f(X)
plt.fill_between(X,Y)
plt.xticks([np.pi/2,3*np.pi/2],['$\pi/2$','$3\pi/2$']); plt.yticks([]);
plt.xlim([0,2*np.pi]); plt.ylim([0,3]);
plt.show()
In our introductory calculus courses, we focus on integrals which we can solve exactly by the Fundamental Theorem of Calculus such as
$$ \int_0^{\pi/2} \cos(x) \, dx = \sin(\pi/2) - \sin(0) = 1 $$
However, most definite integrals are impossible to solve exactly. For example, the famous error function in probability
$$ \mathrm{erf}(x) = \frac{2}{\sqrt{\pi}} \int_0^x e^{-t^2} dt $$
is a definite integral for which there is no explicit formula.
The idea behind numerical integration is to use simple geometric shapes to approximate the area under the curve $y=f(x)$ to estimate definite integrals. In this section, we explore the simplest methods of numerical integration: Riemann sums, the trapezoid rule and Simpson's rule.
Riemann Sums¶
While a definite integral can be fairly straightfoward and we can solve exactly using the Fundamental Theorem of Calculus, other integrals can not be solved exactly (or at least not numerically only).
Definition¶
A Riemann sum of a function $f(x)$ over a partition
$$ x_0 = a < x_1 < \cdots < x_{N-1} < x_N = b $$
is a sum of the form
$$ \sum_{i=1}^N f(x_i^ * ) (x_i - x_{i-1}) \ \ , \ x_i^* \in [x_{i-1},x_i] $$
where each value $x_i^* \in [x_{i-1},x_i]$ in each subinterval is arbitrary.
Riemann sums are important because they provide an easy way to approximate a definite integral
$$ \int_a^b f(x) \, dx \approx \sum_{i=1}^N f(x_i^ * ) (x_i - x_{i-1}) \ \ , \ x_i^* \in [x_{i-1},x_i] $$
Notice that the product $f(x_i^ * ) (x_i - x_{i-1})$ for each $i$ is the area of a rectangle of height $f(x_i^ * )$ and width $x_i - x_{i-1}$. We can think of a Riemann sum as the area of $N$ rectangles with heights determined by the graph of $y=f(x)$.
The value $x_i^*$ chosen in each subinterval is arbitrary however there are certain obvious choices:
- A left Riemann sum is when each $x_i^* = x_{i-1}$ is the left endpoint of the subinterval $[x_{i-1},x_i]$
- A right Riemann sum is when each $x_i^* = x_i$ is the right endpoint of the subinterval $[x_{i-1},x_i]$
- A midpoint Riemann sum is when each $x_i^* = (x_{i-1} + x_i)/2$ is the midpoint of the subinterval $[x_{i-1},x_i]$
Let's visualize rectangles in the left, right and midpoint Riemann sums for the function
$$ f(x) = \frac{1}{1 + x^2} $$
over the interval $[0,5]$ with a partition of size $N=10$.
graph_riemann()
Notice that when the function $f(x)$ is decreasing on $[a,b]$ the left endpoints give an overestimate of the integral $\int_a^b f(x) dx$ and right endpoints give an underestimate. The opposite is true is when the function is increasing.
Let's compute the value of each of the Riemann sums:
dx = (b-a)/N
x_left = np.linspace(a,b-dx,N)
x_midpoint = np.linspace(dx/2,b - dx/2,N)
x_right = np.linspace(dx,b,N)
print("Partition with",N,"subintervals.")
left_riemann_sum = np.sum(f(x_left) * dx)
print("Left Riemann Sum:",left_riemann_sum)
midpoint_riemann_sum = np.sum(f(x_midpoint) * dx)
print("Midpoint Riemann Sum:",midpoint_riemann_sum)
right_riemann_sum = np.sum(f(x_right) * dx)
print("Right Riemann Sum:",right_riemann_sum)
Partition with 10 subintervals. Left Riemann Sum: 1.613488696614725 Midpoint Riemann Sum: 1.373543428316664 Right Riemann Sum: 1.1327194658454942
In this case, we can find a fairly accurate value for:
$$ \int_0^5 \frac{1}{1 + x^2} dx = \arctan(5) $$
While a true value might be off slightly from a hand calculation, it gets really close and we can use that to verify our approximations.
Why is a numerical value done computationally not exact?
I = np.arctan(5)
print(I)
1.373400766945016
print("Left Riemann Sum Error:",np.abs(left_riemann_sum - I))
print("Midpoint Riemann Sum:",np.abs(midpoint_riemann_sum - I))
print("Right Riemann Sum:",np.abs(right_riemann_sum - I))
Left Riemann Sum Error: 0.24008792966970915 Midpoint Riemann Sum: 0.00014266137164820059 Right Riemann Sum: 0.24068130109952168
Error Formulas¶
A Riemann sum is an approximation of a definite integral. A natural question arises: how good of an approximation is a Riemann sum? Let's look at one of the Riemann Theorems.
Theorem. Let $M_N(f)$ denote the midpoint Riemann sum
$$ M_N(f) = \sum_{i=1}^N f(x_i^* ) \Delta x $$
where $\Delta x = (b-a)/N$ and $x_i^* = (x_{i-1} + x_i)/2$ for $x_i = a + i \Delta x$. The error bound is
$$ E_N^{M}(f) = \left| \ \int_a^b f(x) \ dx - M_N(f) \ \right| \leq \frac{(b-a)^3}{24 N^2} K_2 $$
where $\left| \, f''(x) \, \right| \leq K_2$ for all $x \in [a,b]$.
The complete list of theorems for the Riemann sum is left in the notebook for you to review as needed.
Implementation¶
Let's write a function called riemann_sum which takes 5 input parameters f, a, b, N and method and returns the Riemann sum
$$ \sum_{i=1}^N f(x_i^*) \Delta x $$
where $\Delta x = (b-a)/N$ and $x_i = a + i\Delta x$ defines a partition with $N$ subintervals of equal length, and method determines whether we use left endpoints, right endpoints or midpoints (with midpoints as the default method).
def riemann_sum(f,a,b,N,method='midpoint'):
'''Compute the Riemann sum of f(x) over the interval [a,b].
Parameters
----------
f : function
Vectorized function of one variable
a , b : numbers
Endpoints of the interval [a,b]
N : integer
Number of subintervals of equal length in the partition of [a,b]
method : string
Determines the kind of Riemann sum:
right : Riemann sum using right endpoints
left : Riemann sum using left endpoints
midpoint (default) : Riemann sum using midpoints
Returns
-------
float
Approximation of the integral given by the Riemann sum.
'''
dx = (b - a)/N
x = np.linspace(a,b,N+1)
if method == 'left':
x_left = x[:-1]
return np.sum(f(x_left)*dx)
elif method == 'right':
x_right = x[1:]
return np.sum(f(x_right)*dx)
elif method == 'midpoint':
x_mid = (x[:-1] + x[1:])/2
return np.sum(f(x_mid)*dx)
else:
raise ValueError("Method must be 'left', 'right' or 'midpoint'.")
Let's test our function with inputs where we know exactly what the output should be. For example, we know
$$ \int_0^{\pi/2} \sin(x) \, dx = 1 $$
and, since $\sin(x)$ is increasing on $[0,\pi/2]$, we know that left endpoints will give an under-estimate, and right endpoints will give an over-estimate. Which one should we use?
Which one should we use?
riemann_sum(np.sin,0,np.pi/2,100)
1.0000102809119054
riemann_sum(np.sin,0,np.pi/2,100,'right')
1.007833419873582
riemann_sum(np.sin,0,np.pi/2,100,'left')
0.992125456605633
We also know that $\int_0^1 x \, dx = 1/2$ and midpoint should give the result exactly for any $N$:
riemann_sum(lambda x : x,0,1,1)
0.5
Examples¶
Approximate Pi¶
Find a value $N$ which guarantees the right Riemann sum of $f(x)=\frac{4}{1 + x^2}$ over $[0,1]$ is within $10^{-5}$ of the exact value
$$ \int_0^1 \frac{4}{1 + x^2} dx = \pi $$
Compute
$$ f'(x) = -\frac{8x}{(1+x^2)^2} $$
Use brute force optimization to find a bound on $\left| f'(x) \right|$ on $[0,1]$:
x = np.linspace(0,1,1000)
y = np.abs(-8*x/(1 + x**2)**2)
np.max(y)
2.5980759093919907
Therefore, $\left| f'(x) \right| \leq 2.6$ for $x \in [0,1]$. Use the error bound
$$ \frac{(b-a)^2}{2 N} K_1 \leq 10^{-5} \ \Rightarrow \ \frac{1.3}{N} \leq 10^{-5} \ \Rightarrow \ 130000 \leq N $$
Let's compute the right Riemann sum for $N=130000$:
approximation = riemann_sum(lambda x : 4/(1 + x**2),0,1,130000,method='right')
print(approximation)
3.1415849612722386
Verify the accuracy of the approximation
np.abs(approximation - np.pi) < 10**(-5)
True
Approximate ln(2)¶
Find a value $N$ which guarantees the midpoint Riemann sum of $f(x)=\frac{1}{x}$ over $[1,2]$ is within $10^{-8}$ of the exact value
$$ \int_1^2 \frac{1}{x} dx = \ln(2) $$
Compute
$$ f''(x) = \frac{2}{x^3} $$
Since $f''(x)$ is decreasing for all $x>0$ we have $\left| \, f''(x) \, \right| \leq 2$ for all $x \in [1,2]$. Use the error bound:
$$ \frac{(b-a)^3}{24 N^2} K_2 \leq 10^{-8} \ \Rightarrow \ \frac{1}{12 N^2} \leq 10^{-8} \ \Rightarrow \frac{10^4}{\sqrt{12}} \leq N $$
10**4 / np.sqrt(12)
2886.751345948129
Therefore a partition of size $N=2887$ guarantees the desired accuracy:
approximation = riemann_sum(lambda x : 1/x,1,2,2887,method='midpoint')
print(approximation)
0.6931471768105913
Verify the accuracy of the approximation:
np.abs(approximation - np.log(2)) < 10**(-8)
True
Trapezoid Rule¶
The Trapezoid Rule fits a trapezoid into each subinterval and sums the areas of the trapezoid to approximate the total integral. This approximation for the integral to an arbitrary function is shown in the following figure. For each subinterval, the Trapezoid Rule computes the area of a trapezoid with corners at $(x_i, 0), (x_{i+1}, 0), (x_i, f(x_i))$, and $(x_{i+1}, f(x_{i+1}))$, which is $h\frac{f(x_i) + f(x_{i+1})}{2}$. Thus, the Trapezoid Rule approximates integrals according to the expression
$$\int_a^b f(x) dx \approx \sum_{i=0}^{n-1} h\frac{f(x_i) + f(x_{i+1})}{2}.$$
You may notice that the Trapezoid Rule "double-counts" most of the terms in the series. To illustrate this fact, consider the expansion of the Trapezoid Rule:
\begin{align}\sum_{i=0}^{n-1} h\frac{f(x_i) + f(x_{i+1})}{2} &=& \frac{h}{2} \left[(f(x_0) + f(x_1)) + (f(x_1) + f(x_2)) + (f(x_2)\right. \\ &&\left. + f(x_3)) + \cdots + (f(x_{n-1}) + f(x_n))\right].\end{align}
Computationally, this is many extra additions and calls to $f(x)$ than is really necessary. We can be more computationally efficient using the following expression.
$$\int_a^b f(x) dx \approx \frac{h}{2} \left(f(x_0) + 2 \left(\sum_{i=1}^{n-1} f(x_i)\right) + f(x_n)\right).$$
To determine the accuracy of the Trapezoid Rule approximation, we first take Taylor series expansion of $f(x)$ around $y_i = \frac{x_{i+1} + x_i}{2}$, which is the midpoint between $x_i$ and $x_{i+1}$. This Taylor series expansion is
$$f(x) = f(y_i) + f^{\prime}(y_i)(x - y_i) + \frac{f''(y_i)(x - y_i)^2}{2!} + \cdots$$
Example¶
Use the Trapezoid Rule to approximate $\int_0^{\pi} \sin(x) dx$ with 11 evenly spaced grid points over the whole interval. Compare this value to the exact value of 2
a = 0
b = np.pi
n = 11
h = (b - a) / (n - 1)
x = np.linspace(a, b, n)
f = np.sin(x)
I_trap = (h/2)*(f[0] + \
2 * sum(f[1:n-1]) + f[n-1])
err_trap = 2 - I_trap
print(I_trap)
print(err_trap)
1.9835235375094546 0.01647646249054535
Simpson's Rule¶
Consider two consecutive subintervals, $[x_{i-1}, x_i]$ and $[x_i, x_{i+1}]$. Simpson's Rule approximates the area under $f(x)$ over these two subintervals by fitting a quadratic polynomial through the points $(x_{i-1}, f(x_{i-1})), (x_i, f(x_i))$, and $(x_{i+1}, f(x_{i+1}))$, which is a unique polynomial, and then integrating the quadratic exactly. The following shows this integral approximation for an arbitrary function.
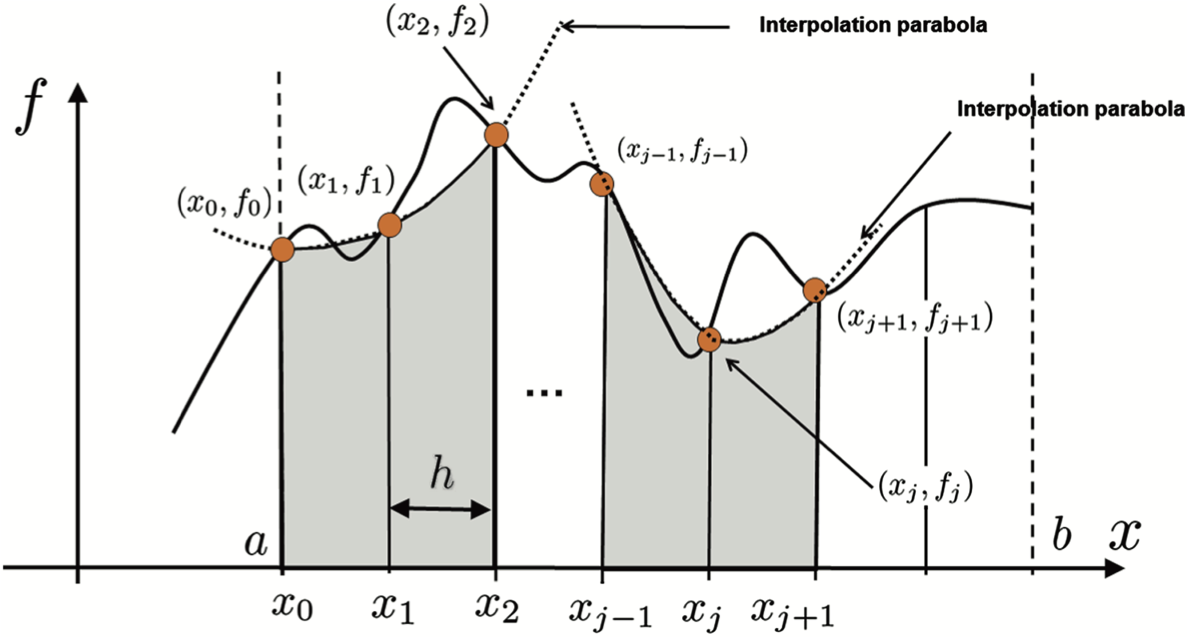
First, we construct the quadratic polynomial approximation of the function over the two subintervals. The easiest way to do this is to use Lagrange polynomials, which was discussed in Chapter 17. By applying the formula for constructing Lagrange polynomials we get the polynomial
\begin{eqnarray*}P_i(x) &=& f(x_{i-1})\frac{(x - x_i)(x - x_{i+1})}{(x_{i-1} - x_i)(x_{i-1} - x_{i+1})} + f(x_i)\frac{(x - x_{i-1})(x - x_{i+1})}{(x_{i} - x_{i-1})(x_{i} - x_{i+1})}\\ &&+ f(x_{i+1})\frac{(x - x_{i-1})(x - x_{i})}{(x_{i+1} - x_{i-1})(x_{i+1} - x_{i})},\end{eqnarray*}
and with substitutions for $h$ results in
$$P_i(x) = \frac{f(x_{i-1})}{2h^2} (x - x_i)(x - x_{i+1}) - \frac{f(x_i)}{h^2} (x - x_{i-1})(x - x_{i+1}) + \frac{f(x_{i+1})}{2h^2} (x - x_{i-1})(x - x_{i}).$$
You can confirm that the polynomial intersects the desired points. With some algebra and manipulation, the integral of $P_i(x)$ over the two subintervals is
$$\int_{x_{i-1}}^{x_{i+1}} P_i(x) dx = \frac{h}{3}(f(x_{i-1}) + 4f(x_i) + f(x_{i+1}).$$
To approximate the integral over $(a, b)$, we must sum the integrals of $P_i(x)$ over every two subintervals since $P_i(x)$ spans two subintervals. Substituting $\frac{h}{3}(f(x_{i-1}) + 4f(x_i) + f(x_{i+1}))$ for the integral of $P_i(x)$ and regrouping the terms for efficiency leads to the formula
$$\int_a^b f(x) dx \approx \frac{h}{3} \left[f(x_0)+4 \left(\sum_{i=1, i\ {\text{odd}}}^{n-1}f(x_i)\right)+2 \left(\sum_{i=2, i\ {\text{even}}}^{n-2}f(x_i)\right)+f(x_n)\right].$$
This regrouping is illustrated in the figure below:
![Illustration of the accounting procedure to approximate the function f by the Simpson rule for the entire interval [a, b]. Regrouping](images/21.04.2-Simpson_integral_2.png)
Example¶
Use Simpson's Rule to approximate $\int_{0}^{\pi} \text{sin} (x)dx$ with 11 evenly spaced grid points over the whole interval. Compare this value to the exact value of 2.
a = 0
b = np.pi
n = 11
h = (b - a) / (n - 1)
x = np.linspace(a, b, n)
f = np.sin(x)
I_simp = (h/3) * (f[0] + 2*sum(f[:n-2:2]) \
+ 4*sum(f[1:n-1:2]) + f[n-1])
err_simp = 2 - I_simp
print(I_simp)
print(err_simp)
2.0001095173150043 -0.00010951731500430384
Solving with SciPy in Python¶
The $scipy.integrate$ sub-package has several functions for computing integrals. The $trapz$ takes as input arguments an array of function values $f$ computed on a numerical grid $x$.
🚀 In-Class Exercise¶
Use the $trapz$ function to approximate $\int_{0}^{\pi}\text{sin}(x)dx$ for 11 equally spaced points over the whole interval. Compare this value to the one computed in the early example using the Trapezoid Rule.
from scipy.integrate import trapz
a = 0
b = np.pi
n = 11
h = (b - a) / (n - 1)
x = np.linspace(a, b, n)
f = np.sin(x)
#INSERT YOUR CODE BELOW
#################
print(I_trapz)
print(I_trap)
Sometimes we want to know the approximated cumulative integral. That is, we want to know $F(X) = \int_{x_0}^X f(x) dx$. For this purpose, it is useful to use the $cumtrapz$ function $cumsum$, which takes the same input arguments as $trapz$.
🚀 In-Class Exercise¶
Use the $cumtrapz$ function to approximate the cumulative integral of $f(x) = \text{sin}(x)$ from $0$ to $\pi$ with a discretization step of 0.01. The exact solution of this integral is $F(x) = sin(x)$. Plot the results.
from scipy.integrate import cumtrapz
x = np.arange(0, np.pi, 0.01)
F_exact = -np.cos(x)
The $quad(f,a,b)$ function uses a different numerical differentiation scheme to approximate integrals. $quad$ integrates the function defined by the function object, $f$, from $a$ to $b$.
🚀 In-Class Exercise¶
Use the $integrate.quad$ function to compute $\int_{0}^{\pi} \text{sin}(x)dx$. Compare your answer with the correct answer of 2.
from scipy.integrate import quad