We have discussed Complexity briefly, but let's dive deeper into the topic. In addition, let's talk about debugging, what that means, and some things you can do to check your work.
- Complexity
- Debugging
- Unit Testing
With complexity, we examine two things typically:
- Time – How fast (in general) or efficient our algorithm is
- Space - How much space it takes up (RAM)
When we look at complexity we examine, in general, what the time and storage requirements are.
- Big O doesn’t show the time it takes for a program or algorithm to run; it shows how many operations it will take.
- Recall that a computer requires many steps to perform a function
- Clock speed can vary; operations can not
Complexity and Big-O Notation¶
The complexity of a function is the relationship between the input size and the difficulty of running the function to completion. The size of the input is usually denoted by $n$. However, $n$ usually describes something more tangible, such as the length of an array. The difficulty of a problem can be measured in several ways.
One suitable way to describe the problem's difficulty is to use basic operations: additions, subtractions, multiplications, divisions, assignments, and function calls. Although each essential operation takes different amounts of time, the number of basic operations needed to complete a function is sufficiently related to the running time to be helpful, and it is much easier to count.
Example¶
Count the number of basic operations, in terms of $n$, required for the following function to terminate.
def f(n):
out = 0
for i in range(n):
for j in range(n):
out += i*j
return out
Let's calculate the number of operations:
additions: $n^2$, subtractions: 0, multiplications: $n^2$, divisions: 0, assignments: $2n^2 +1$, function calls: 0, total: $4n^2+1$.
The number of assignments is $2n^2 + n + 1$ because the line $out += i*j$ is evaluated $n^2$ times, $j$ is assigned $n^2$, $i$ is assigned $n$ times, and the line $out = 0$ is assigned once. So, the complexity of the function $f$ can be described as $4n^2 + n + 1$.
A standard notation for complexity is called Big-O notation. Big-O notation establishes the relationship in the growth of the number of basic operations concerning the input size as the input size becomes vast. Since hardware differs on every machine, we cannot accurately calculate how long it will take to complete without evaluating the hardware. Then, that analysis is only suitable for that specific machine. We do not care how long a particular set of input on a specific machine takes. Instead, we will analyze how quickly "time to completion" in basic operations grows as the input size grows because this analysis is hardware-independent. As $n$ gets large, the highest power dominates; therefore, only the highest power term is included in Big-O notation. Additionally, coefficients are not required to characterize growth, and so coefficients are also dropped.
Looking at the previous example, we had $4n^2 + n + 1$. But, the 4 in front of the $n^2$ does not affect the complexity as the $n^2$ has a much stronger effect so that we can ignore that. This is true for both $n$ and the $+1$. So, the complexity is simplified to $n^2$ or as written as Big O notation $O(n^2)$.
🎩 In-Class Exercise¶
Determine the complexity of the iterative Fibonacci function in Big-O notation. Answer in Tophat.
def my_fib_iter(n):
out = [1, 1]
for i in range(2, n):
out.append(out[i - 1] + out[i - 2])
return out
Since the only lines of code that take more time as $n$ grows are those in the for-loop, we can restrict our attention to the for-loop and the code block within it. The code within the for-loop does not increase concerning $n$ (i.e., it is constant). Therefore, the number of basic operations is $Cn$ where $C$ is some constant representing the number of basic operations that occur in the for-loop, and these $C$ operations run $n$ times. This gives a complexity of $O(n)$ for $my\_fib\_iter$.
Assessing the exact complexity of a function can be difficult. In these cases, giving an upper bound or even an approximation of the complexity might be sufficient.
🚀 In-Class Exercise¶
Give an upper bound on the complexity of the recursive implementation of Fibonacci. Do you think it is a good approximation of the upper bound? Do you think that recursive Fibonacci could possibly be polynomial time?
def my_fib_rec(n):
if n < 2:
out = 1
else:
out = my_fib_rec(n-1) + my_fib_rec(n-2)
return out
As $n$ gets large, we can say that the vast majority of function calls make two other function calls: one addition and one assignment to the output. The addition and assignment do not grow with $n$ per function call, so we can ignore them in Big-O notation. However, the number of function calls grows approximately by $2^n$ , and so the complexity of $my\_fib\_rec$ is upper bound by $O(2^n)$.
There is on-going debate whether or not $O(2^n)$ is a good approximation for the Fibonacci function.
Since the number of recursive calls grows exponentially with $n$, there is no way the recursive fibonacci function could be polynomial. That is, for any $c$, there is an $n$ such that $my\_fib\_rec$ takes more than $O(n^c)$ basic operations to complete. Any function that is $O(c^n)$ for some constant c is said to be exponential time.
🚀 In-Class Exercise¶
What is the complexity of the following function in Big-O notation?
def my_divide_by_two(n):
out = 0
while n > 1:
n /= 2
out += 1
return out
Again, only the while-loop runs longer for larger $n$ so that we can restrict our attention there. Within the while-loop are two assignments: one division and one addition, which are both constant time with respect to $n$. So, the complexity depends only on how many times the while-loop runs.
The while-loop cuts $n$ in half in every iteration until $n$ is less than 1. So the number of iterations, $I$, is the solution to the equation $\frac{n}{2^I} = 1$. With some manipulation, this solves to $I = \log n$, so the complexity of $my\_divide\_by\_two$ is $O(log n)$. It does not matter what the base of the log is because, recalling log rules, all logs are a scalar multiple of each other. Any function with complexity $O(\log n)$. is said to be log time.
Complexity Matters¶
So why does complexity matter? Because different complexity requires different time to complete the task. The following figure is a quick sketch showing you how the time changes with different input size for complexity $log(n)$, $n$, $n^2$.
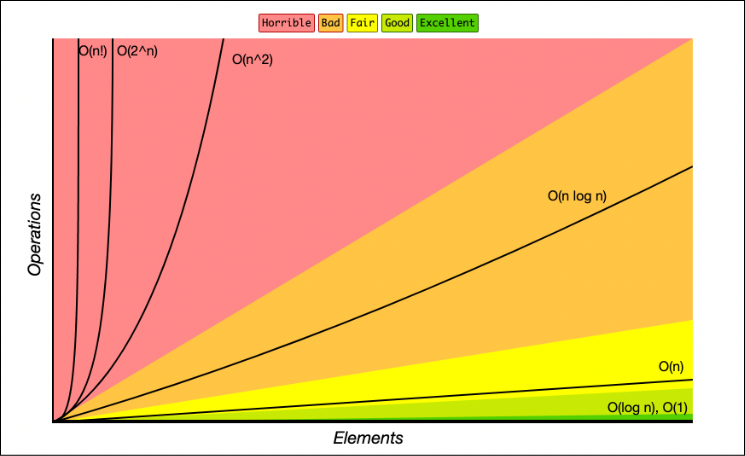
Let us look at another example. Assume you have an algorithm that runs in exponential time, say $O(2^n)$, and let $N$ be the largest problem you can solve with this algorithm using the computational resources you have, denoted by $R$. $R$ could be the amount of time you are willing to wait for the function to finish, or $R$ could be the number of basic operations you watch the computer execute before you get sick of waiting. Using the same algorithm, how large of a problem can you solve given a new computer that is twice as fast?
If we establish $R = 2^N$, using our old computer, with our new computer, we have $2R$ computational resources; therefore, we want to find $N^{\prime}$ such that $2R = 2^{N^{\prime}}$. With some substitution, we can arrive at $2 \times 2^N = 2^{N^{\prime}}\rightarrow 2^{N+1} = 2^{N^{\prime}}\rightarrow N' = N+1$. So with an exponential time algorithm, doubling your computational resources will allow you to solve a problem one unit larger than you could with your old computer. This is a minimal difference. In fact, as $N$ gets large, the relative improvement goes to 0.
With a polynomial time algorithm, you can do much better. This time, let's assume that $R = N^c$, where $c$ is some constant larger than one. Then $2R = {N^{\prime}}^c$, which using similar substitutions as before gets you to $N^{\prime} = 2^{1/c}N$. So, with a polynomial time algorithm with power $c$, you can solve a problem $\sqrt[c]{2}$ larger than you could with your old computer. When $c$ is small, say less than 5, this is a much bigger difference than with the exponential algorithm.
Finally, let us consider a log time algorithm. Let $R = \log{N}$. Then $2R = \log{N^{\prime}}$, and again with some substitution we obtain $N^{\prime} = N^2$. So, with the double resources, we can square the size of the problem we can solve!
The story's moral is that exponential time algorithms do not scale well. As you increase the input size, you will soon find that the function takes longer (much longer) than you are willing to wait. For one final example, $my\_fib\_rec(100)$ would take on the order $2^{100}$ basic operations to perform. If your computer could do 100 trillion basic operations per second (far faster than the fastest computer on earth), it would take your computer about 400 million years to complete. However, $my\_fib\_iter(100)$ would take less than one nanosecond.
There is an exponential time algorithm (recursion) and a polynomial time algorithm (iteration) for computing Fibonacci numbers. Given a choice, we would pick the polynomial time algorithm. However, there is a class of problems for which no one has ever discovered a polynomial time algorithm. In other words, there are only exponential time algorithms known for them. These problems are known as NP-complete, and there is ongoing investigation on whether polynomial time algorithms exist for these problems. Examples of NP-complete problems include the Traveling Salesman, Set Cover, and Set Packing problems. However, theoretical construction solutions to these problems have numerous applications in logistics and operations research. Some encryption algorithms that keep web and bank applications secure rely on the NP-Complete-ness of breaking them. A further discussion of NP-complete problems and the theory of complexity is beyond the scope of this book. Still, these problems are very interesting and important to many engineering applications.
plt.figure(figsize = (12, 8))
n = np.arange(1, 1e3)
plt.plot(np.log(n), label = 'log(n)')
plt.plot(n, label = 'n')
plt.plot(n**2, label = '$n^2$')
plt.yscale('log')
plt.legend()
plt.show()

Debugging¶
- History
- Admiral Grace Hopper
- Literally found a bug
- Debugging is the process of finding compile time and run time errors in the code.
- Compile/Run time errors occur due to misuse of Python language constructs.
- Most of the compile/run time errors can be overcome with careful attention to language syntax and use.
- Finding syntax errors is the first step in a debugging process.
- Missing/misplaced semicolons
- Common in early development
- Does not go on loops
- Compiler will tell you about this
Debugging is the process of systematically removing errors or bugs from your code. Python has functionalities that can assist you when debugging. The standard debugging tool in Python is pdb (Python DeBugger) for interactive debugging. It lets you step through the code line by line to find out what might be causing a difficult error. The Ipython version of this is ipdb (IPython DeBugger). We won't cover too much about it here; you can check out the documentation for details. In this section, basic debug steps in Jupyter Notebook will be introduced. We will show you how to use two handy magic commands %debug and %pdb to find out the trouble code.
There are two ways you could debug your code: (1) activate the debugger after you run into an exception; (2) activate the debugger before we run the code.
Activate the debugger after we run into an exception¶
If we run the code that stops at an exception, we could call %debug. For example, we have a function that squares the input number and then adds itself, as shown below:
def square_number(x):
sq = x**2
sq += x
return sq
square_number('10')
--------------------------------------------------------------------------- TypeError Traceback (most recent call last) Cell In[30], line 1 ----> 1 square_number('10') Cell In[28], line 3, in square_number(x) 1 def square_number(x): ----> 3 sq = x**2 4 sq += x 6 return sq TypeError: unsupported operand type(s) for ** or pow(): 'str' and 'int'
After we have this exception, we could activate the debugger by using the magic command - %debug, which will open an interactive debugger for you. You can type in commands in the debugger to get useful information.
%debug
> /var/folders/rq/kct3v3md3x79drbqvbswb6wc0000gn/T/ipykernel_40483/776842912.py(3)square_number() 1 def square_number(x): 2 ----> 3 sq = x**2 4 sq += x 5
ipdb> h
Documented commands (type help <topic>): ======================================== EOF commands enable list pinfo2 rv unt a condition exceptions ll pp s until alias cont exit longlist psource skip_hidden up args context h n q skip_predicates w b continue help next quit source whatis break d ignore p r step where bt debug interact pdef restart tbreak c disable j pdoc return u cl display jump pfile retval unalias clear down l pinfo run undisplay Miscellaneous help topics: ========================== exec pdb
ipdb> q
You can see that after we activate the ipdb, we could type commands to get the information of the code. The example above, I typed the following commands:
- h to get a list of help
- p x to print the value of x
- type(x) to get the type of x
- p locals() to print out all the local variables
There are some most frequent commands you can type in the pdb, like:
- n(ext) line and run this one
- c(ontinue) running until next breakpoint
- p(rint) print varibles
- l(ist) where you are
- 'Enter' Repeat the previous command
- s(tep) Step into a subroutine
- r(eturn) Return out of a subroutine
- h(elp) h
- q(uit) the debugger
Activate debugger before we run the code¶
We could also turn on the debugger before we even run the code and then turn it off after we finish running the code.
%pdb on
Automatic pdb calling has been turned ON
square_number('10')
--------------------------------------------------------------------------- TypeError Traceback (most recent call last) Cell In[37], line 1 ----> 1 square_number('10') Cell In[28], line 3, in square_number(x) 1 def square_number(x): ----> 3 sq = x**2 4 sq += x 6 return sq TypeError: unsupported operand type(s) for ** or pow(): 'str' and 'int'
> /var/folders/rq/kct3v3md3x79drbqvbswb6wc0000gn/T/ipykernel_40483/776842912.py(3)square_number() 1 def square_number(x): 2 ----> 3 sq = x**2 4 sq += x 5
ipdb> q
# let's turn off the debugger
%pdb off
Automatic pdb calling has been turned OFF
Add a breakpoint¶
It is often very useful to insert a breakpoint into your code. A breakpoint is a line in your code at which Python will stop when the function is run.
import pdb
def square_number(x):
sq = x**2
# we add a breakpoint here
pdb.set_trace()
sq += x
return sq
square_number(3)
> /var/folders/rq/kct3v3md3x79drbqvbswb6wc0000gn/T/ipykernel_40483/1872377299.py(8)square_number() 6 pdb.set_trace() 7 ----> 8 sq += x 9 10 return sq
ipdb> q
We could see after we added pdb.set_trace(), the program stops at this line, and activate the pdb debugger. We could check all the variable values that assigned before this line. And use the command c to continue the execution.
Using the Python's debugger can be extremely helpful in finding and fixing errors in your code. We encourage you to use the debugger for large programs.
